C.C.T. 21DCT0302P
Carrera: Técnico en ofimática
Materia: Calculo Integral
Actividad: Blog
Docente: Ing. Raquel Reyes Banda
Integrantes: Daniela Álvarez Ramírez, Mariana Perez Castro, Karla Yanely Reyes Gonzalez, Jesús Hernán
5° “G”
Semestre: Agosto 2019 – Enero 2020
CALCULO INTEGRAL
El calculo integral es la rama de las matemáticas que tiene como objetivo el abarcar el proceso accidentario también conocido como integración, generalmente se utiliza para determinar el área pajo la curva de una función o el volumen que ocupa una figura en el plano.
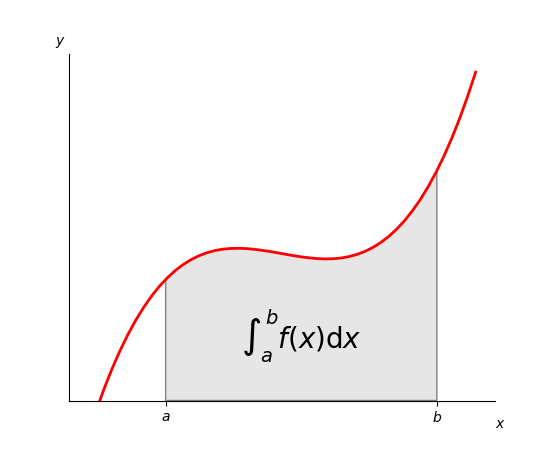
ÁREA BAJO LA CURVA


























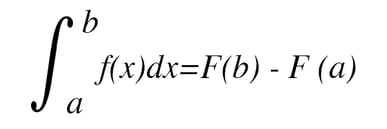
∫2−1(x2+3)dx
=x33+3x|2−1
=((2)33+3(2))−((−1)33+3(−1))
=(83+6)−(−13−3)=83+6+13+3=12u2
Ejemplos de integrales





El volumen es el espacio físico que ocupa un cuerpo, la unidad de volumen está representada por el m3 (metros cúbicos).
La formulación del área bajo una curva es el primer paso para desarrollar el concepto de integral. El área bajo la curva formada por el trazo de la función f(x) y el eje x se puede obtener aproximadamente, dibujando rectángulos de anchura finita y altura f igual al valor de la función en el centro del intervalo.
Si hacemos más pequeño la anchura del rectángulo, entonces el número N es mas grande y mejor la aproximación al valor del área.
1.
Calcular el área limitada por la curva y = x2 − 5x + 6 y la recta y = 2x.
En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites de integración.


De x = 1 a x = 6, la recta queda por encima de la parábola.


2.
Calcular el área limitada por la parábola y2 = 4x y la recta y = x.


De x = o a x = 4, la parábola queda por encima de la recta.

3.
Calcular el área limitada por las gráficas de las funciones 3y =x2 e y = −x2 + 4x.
En primer lugar representamos las parábolas a partir del vértice y los puntos de corte con los ejes.





Hallamos también los puntos de corte de las funciones, que nos darán los límites de integración.




4.
Calcula el área de la figura plana limitada por las parábolas y= x2 − 2x, y = −x2 + 4x.
Representamos las parábolas a partir del vértice y los puntos de corte con los ejes.










INTEGRALES DEFINIDAS E INDEFINIDAS
En matemáticas, la integración es la forma de resolver, desde el cálculo integral, dos problemas clásicos del Análisis Matemático, estrechamente relacionados:
- El cálculo de áreas y volúmenes de figuras geométricas conocidas.
- La obtención de la primitiva de una función, esto es, aquella cuya derivada es la función dada, realizando la "operación inversa" a la derivación.
Los estudios de Isaac Barrow, Isaac Newton y Gottfried Leibniz, dieron forma al teorema fundamental del cálculo, que establece la íntima relación en la solución de ambos problemas. Se denomina integración definida a la obtención del área bajo una curva, e integración indefinida a la operación inversa de la derivación. También se denomina integración a la resolución de una ecuación diferencial, una ecuación en la que la incógnita es una o varias funciones y sus derivadas.
La integral definida, como en su nombre dice, está definida en un cierto intervalo, es decir [a,b], donde [a,b] ∈ R a,b ∈ ℜ (a y b pertenecen a los reales). Una de sus utilidades, es que a través de la integral definida, podemos obtener áreas.
TIENE LA FORMA:

La diferencia de una integral indefinida a una definida, es que terminando de integrar, en lugar de colocar al final del resultado, más una constante (+C), se realiza una resta de evaluaciones.
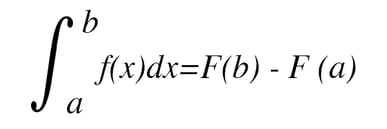
EJEMPLO:
El resultado de
1. Primero se debe de integrar la expresión, en este caso se hará de manera directa:
2. Después de haber integrado, se comienza a evaluar la variable por los valores que definen a la integral. Se empieza evaluando primero con 2 y se resta la evaluación con -1.
3. Por último, se realizan las operaciones aritméticas para llegar a un resultado numérico.
Ejemplos de integrales
1. Definida

Usamos las formulas definidas para integrar la función 


Ahora , lo siguiente es evaluar esa función en los puntos 0 y 2:


2.Indefinida
VOLUMEN
|
El volumen corresponde al espacio que la forma ocupa, por lo tanto, es la multiplicación de la altura por el ancho y por el largo. El volumen sirve, por ejemplo, cuando queremos calcular la cantidad de agua en una piscina.

DERIVADAS
DEFINICIÓN Sea y f(x) una función dada. La derivada de y con respecto a x,
denotada por dy/dx, se define por.
con tal de que este límite exista.
A la derivada también se le da el nombre de coeficiente diferencial y la operación
de calcular la derivada de una función se denomina diferenciación.
Si la derivada de una función existe en un punto particular, decimos que f es
diferenciable en tal punto.
URL DE FUENTES DE INFORMACIÓN
FUENTES DE INFORMACIÓN
- Libreta de apuntes



No hay comentarios.:
Publicar un comentario